11 Числовые характеристики. Характеристики рассеяния.
II) характеристики рассеяния (разброса). Дисперсией (рассеянием) св Х наз-ся матем. ожид. квадрата ее отклонения. D(x)=DX=M(x¢² )=M[(x-M(x))² ]. Х-ДСВ ^x/_p|^x1,x2…xn /_p1,p2…pn .D(x)=S(xi-M(x))² *pi= (x1-M(x))²  *p1+ …+(xn-M(x))²  *pn.Х-НСВ с ¦(х).D(x)=ò(x-M(x))² *¦(х)*dx. 1° D(c)=0;2° D(c*x)=c² D(x)4; 3°если св Х и У – независимы, то D(Х+У) = D(Х)+ D(У) из этого св-ва вытекают 1сл: D(Х-У)= D(Х)+ D(У),2сл: х1, х2,…,хn попарно независимы то D(х1, х2,…,хn)= D(х1)+ D(х2)+…+ D(хn), 3сл: если х1, х2,…,хn- независимы в совок-ти то D(Sxi)=SD(xi). 4° D(x)=M((x-M(x))² =M(x² -2*X*M(X)+ M(x))² )= M(x² )- [M(x)]² . 5°:`х= (х1+х2+…+хn)/n. М(`х)=1/n (M(x1)+…+M(xn)). D(`х)=1/n<sup>2</sup> (D(x1)+…+D(xn)), если D(x1)=D(x2)=…=D(xn)=D(x), то D(`х)=1/n²*n*D(х)=D(х)/n. Дисперсия имеет размерность квадрата св. s(х)=+ÖD(x) – среднее квадратическое отклоние или стандарт. g=s(х)/М(х)*100% - коэффициент вариации (рассеяния). Он показывает на сколько велико рассеивание возможных значений св по сравнению с мат. ожид-ем. Этот показатель использ. тогда когда среднее значение существенно.

III)моменты. Обобщением мат.ожидания и дисперсии яв-ся моменты. Бывают начальные и центральные. Начальным моментом k-ого порядка наз-ся мат.ожидание х в степени k (n_k =M(X^k)). При k=1, n =M(X); при k=2, n₂ =M(X²). Х-ДСВ, то n_k=Sх^k_i*p_i; если Х-НСВ, n_k =òх^k *¦(x)dx. Центральным моментом k-ого порядка наз-ся математическое ожидание k-ой степени отклонения:m_k =M(x¢^k )=M[(x-M(x))^k ]; k=1: m₁=0; k=2: m₂=D(X)= M((x-M(x))² );

m₂ =n₂-(n₁)²

m₃ =n₃-3n₁n₂+2n₁³

m₄ =n₄-4n₃n₁+6n₂n₁²-3n₁⁴

m₅ и т.д. – обладают очень большим разбросом

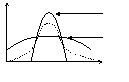
m₃ – яв-ся характеристикой ассиметрии (скошенности распределения СВ). если СВ распределена симметрично относительно мат.ожидания то m₃=0. если m₃>0, то длинная часть кривой распределения лежит справа. В том случае говорят, что СВ имеет положительную ассиметрию, если m₃<0, то имеем отрицательную ассиметрию.

m₃ имеет размерность куба 1 СВ поэтому в рассмотрении вводят безразмерную величину называемую коэфиц. ассиметрии или коэф.скошенности. А=m₃ /s³. в качестве харак-ки большей или меньшей вершинности используется центральный момент 4-ого порядка.

E=(m₄/s⁴)-3 – эксцесс.

Кроме указанных моментов сущ. абсолютный начальный момент и абсолютный центральный момент.a_k=M|X|^k; b_k=M|X¢|^k. Среди этих моментов b₁ =M|X-M(X)| служит характеристикой рассеяния значений СВ относительно среднего значения.