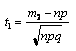13. Повторные испытания. Формула Бернулли. Биномиальное распределение. Локальная и интегральная формулы Муавра-Лапласа

Схема испытаний Бернулли, биномиальное распределение.

Рассм серию повторных испытаний. Пусть результат каждого испытания есть появление одного из 2-х альтерн исходов. Наступление некот события A или противополож ему событию . Испыт могут проводится:

1.  когда результат каждого испыт не зависит от предшеств испыт (такие испыт назыв независим)

2.  результат испыт зависит от рез-ов предыд испыт (зависимые испыт)

Независим испыт в свою очередь могут произв в одинаковых или различных условиях. В первом случае P(A) одна и та же во всех испытаниях. Во-втором случае P(A) изменяется от испытания к испытанию.

Задача. Производится n независим испытаний, найти вероятность того, что при этом A появл ровно m раз. Эту вероят обозн

-событие, состоящее в том, что событие A в n испыт наступит ровно m раз. Обозн через и - появление или непоявление события A в i-ом испытании.

- формула Бернулли.

Биномиальное распределение. ДСВ X имеет биномиальное распр, если она приним возм знач 0,1,2,...,n вероятностями M(x)=np; D(x)=npq. Биномиальное распр явл отражением случ эксперимента когда последний можно представить в виде суммы 2-х точечного распр (закон Бернулли).

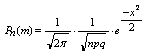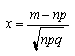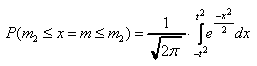, где -локальная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа: , где 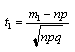,