19. ХИ-квадрат-, t-, F-распределения.

1. ХИ-квадрат распределение.

X~N(a,), -нормированная (стандартизованная) СВ.

- закон распределения СВ ХИ-квадрат наз-ся ХИ-квадрат распред. Со степенью свободы .

Рассмотрим n-независ. СВ Х1, Х2, ..., Хn, распределённых по нормальному закону Xi~N(ai,i) (i=). Составим нормированные СВ.

.

Составим СВ, которую обозначим через ХИ-квадрат:

.

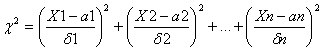Закон распред. СВ ХИ-квадрат наз-ся распред. со степенью свободы

Степень свободы определяется как разность между числом суммируемых СВ число линейных связей, ограничивающих изменения этих СВ.

.

Квантилем ХИ-квадрат распред., при уровне значимости ,

 наз-ся такое значение СВ ХИ-квадрат, обзначаемое , что справедливо       следующее утверждение:

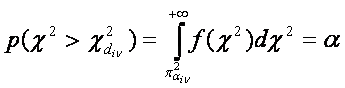
2. Распределение Стьюдента (t-распределение).

Имеем СВ Y, X1, X2, ..., Xn ~ N(0;1).

Составим дробь:

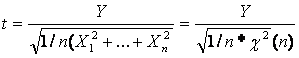
Безразмерная дробь Стьюдента.

t-СВ.

Закон распред. СВ t наз-ся распределением Стьюдента, или t-распеделением.

t-распределение как и ХИ-квадрат табулирована.

Квантилем t-распед. наз-ся такие значения СВ t, обознач. при уровне значимости

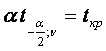
такие, что p(t>)= и p(t<)=

3. Распределение Фишера (F-распределение).

Возьмём незав. СВ X1, X2, ..., Xn ~ N(0;1), Y1, Y2, ..., Yn ~ N(0;1). Составим безразмерную величину, которую обозначим через F:

Закон распред. СВ F наз-ся распред. Фишера (Фишера-Снедокера) со степенью свободы

.

Значения СВ F табулированы и при краткой записи F-распределения сначала указывают степень свободы числителя, имеющего наибольшую дисперсию.

Кривая Фишера строится к нормальному закону распределения.

Квантилью F-распред., при вероятности , наз-ся такое значение СВ F обознач. , такое, что справедливо равенство: