20. —истемы случайных величин. –аспределение двумерной дискретной случайной величины.

20. —истемы случайных величин. –аспределение двумерной дискретной случайной велчины.

X1,X2,Е,Xn

Xi(i=)

=(X1,X2,ЕXn)

X1,X2,Е,Xn-компоненты или координаты

≈сли все составл¤щие системы суть-дискретне —¬, то говор¤т, что имеем систему дискретных —¬ (ƒ—¬), а если сост.-непрер. —¬, то системой непрер. —¬. –азличают смешанные системы, когда одна часть-дискр., а друга¤-непрерывна¤.

«аконом распред. системы —¬ наз-с¤ соотнош., св¤зывающее область возможных значений этой системы и веро¤тности, с которыми система принимает опред. конкретное значение из этой области.

—оставим закон распред. системы 2-х дискретны величин.

—истема (X,Y) наз-с¤ дискретной, если еЄ состав. принимают конечное или счЄтное множество значений.

“аблица распределени¤ системы 2-х дискретных —¬:

X Y	y1	y2	Е	yi	Е	yn
x1	p11	P12	Е	P1j	Е	P1m	P1
x2	P21	P22	Е	P2j	Е	P2m	P2
Е	Е	Е	Е	Е	Е	Е	Е
xi	Pi1	Pi2	Е	Xij	Е	Pim	Pi
Е	Е	Е	Е	Е	Е	Е	Е
xn	Pn2	Pn2	Е	Pnj	Е	pnm	Pn
qi	Q1	Q2	Е	Qij	Е	Qn	1

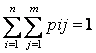
p1=p11+p12+Е+pm=p(X=xi)

X x1 x2 Е xn

p p1 p2 Е pn 1

X Y	y1	y2	Е	yi	Е	yn
x1	p11	P12	Е	P1j	Е	P1m	P1
x2	P21	P22	Е	P2j	Е	P2m	P2
Е	Е	Е	Е	Е	Е	Е	Е
xi	Pi1	Pi2	Е	Xij	Е	Pim	Pi
Е	Е	Е	Е	Е	Е	Е	Е
xn	Pn2	Pn2	Е	Pnj	Е	pnm	Pn
qi	Q1	Q2	Е	Qij	Е	Qn	1

X Y	y1	y2	Е	yi	Е	yn
x1	p11	P12	Е	P1j	Е	P1m	P1
x2	P21	P22	Е	P2j	Е	P2m	P2
Е	Е	Е	Е	Е	Е	Е	Е
xi	Pi1	Pi2	Е	Xij	Е	Pim	Pi
Е	Е	Е	Е	Е	Е	Е	Е
xn	Pn2	Pn2	Е	Pnj	Е	pnm	Pn
qi	Q1	Q2	Е	Qij	Е	Qn	1

X Y	y1	y2	Е	yi	Е	yn
x1	p11	P12	Е	P1j	Е	P1m	P1
x2	P21	P22	Е	P2j	Е	P2m	P2
Е	Е	Е	Е	Е	Е	Е	Е
xi	Pi1	Pi2	Е	Xij	Е	Pim	Pi
Е	Е	Е	Е	Е	Е	Е	Е
xn	Pn2	Pn2	Е	Pnj	Е	pnm	Pn
qi	Q1	Q2	Е	Qij	Е	Qn	1