22. Закон распределения составляющих двумерной случайной величины.

Задача 1.

Дана система 2-х СВ с известным законом распределения. Требуется найти законы распределения составляющих.

(X,Y) F(x,y)

Если система содержит дискретные СВ, то последний столбец и последняя строка таблицы распределения определяют законы распределения составляющих. Если же система содержит непрерывные СВ, то функции распределения могут быть определены след. образом:

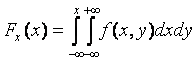
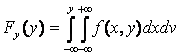
Продифференцировав функции распред. по x и y получаем плотности распред. соотв. составляющих X и Y:

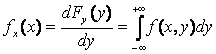
Задача 2.

Зная законы распределения составляющих системы, можно ли найти закон распределения самой системы.

а) если СВ X и Y-независимы (они наз-ся независимыми, есл независимы события)

F(x,y)=.

F(x,y)= .

p(xi,yi)=p(xi)*p(yi).

б) пусть Х и Y-зависимые СВ, тогда, зная законы распределения составляющих вообще говоря, нельзя найти законы распред. самой системы. Причина в том, что между СВ X и Y существует связь, знание которой необх. для решеня задачи.

Для нахождения закона распределения системы введём понятие условный закон распределения составляющей.

УЗР одной из составляющих наз-ся её закон распределения, найденный при условии, что другая составляющая приняла определённое значение.

Закон распределения системы:

(X,Y)

F(x,y)=

F(x,y)=     (1)

f(x,y)=

f(x,y)=

Выражения (1) получили название формула умножения плотностей.