24. Зависимые и независимые случайные величины. Корреляция и коэффициент корреляции. Ковариационная и корреляционная матрицы случайного вектора.
Между СВ существует связь. Если она очень незаметна, то говорят, что СВ независимы.
Иногда между ними существует очень тесная связь, причём знание одной СВ позволяет найти значение другой СВ. В этом случае говорят, что они зависимы, причём зависимость функциональная.
Как охарактеризовать связь между СВ X и Y. Для этого применяется
![]()
![]() ,
X и Y-зависимые.
,
X и Y-зависимые.
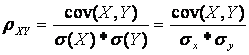
Коэффициент корреляции.
Он показывает тесноту линейной связи между переменными X и Y.
1. Если X и Y-независимые СВ, то
![]() =0
=0
2. ![]()
3. ![]()
4. ![]()
5. ![]() ,
,
![]() ;
;
![]() -нормированные
СВ.
-нормированные
СВ.
6. ![]()
7. ![]() ,
в среднем возрастают одновременно
,
в среднем возрастают одновременно
8. ![]() ,
с увеличением одной величины, другая в среднем уменьшается
,
с увеличением одной величины, другая в среднем уменьшается
9. ![]()
10.
Если X и Y распределены не нормально, то вводят между СВ X
и Y корреляционную зависимость. СВ X и Y наз-ся коррелированными, если
![]() и
некоррелированными, если
и
некоррелированными, если ![]()
Из некоррелированности СВ не следует их независимость, при этом, между переменными могут существовать нелинейные связи.
K= -ковариационная
матрица
-ковариационная
матрица
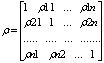 -корреляционная
матрица
-корреляционная
матрица