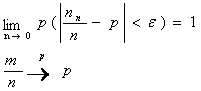
26. Теорема Бернулли. Центральная предельная терема.

Пусть производится n независимых испытаний в каждом из которых событие а производится с вероятностю р. Пусть n-ое число появлений события а в n испытаний, тогда для всех  >0 выполняется равенство     

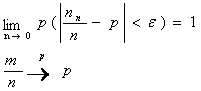
Обозначим через Х_к СВ-число появлений события А в к-том испытании() все эти СВ яв-ся попарно-независимыми и имеют один и тот же закон распределения.

М(х₁) =…М(х_n)=p

D(х₁)=…=D(х_n) =pq

D(х₁)=…D(х_n)≤1/n(p=1/2,1-p=1/2),то применяя 2 теорему Чебышева к событию

Центральная предельная теорема

Любая группа предельных теорем в теории вероятности получила назв-ие центральная предельная теорема сущ-ют различн.формулировки центральной предельной теоремы

Суммы независимых СВ имеет нормальный закон распределения,если: 1)СВ имеют кончные мат.ожидания и дисперсии 2)не одна из случайных величин существенно не отличается от других.