33. Интервальное оценивание. Примеры.

2 подхода к рассм-ю инт. оценок:

-Байесовский

-Фон-Неймана(«Интерв. подходом»)

Пусть  явл-ся  точечн. оценкой неизв. параметра .  тем ближе к , чем меньше разность между ними:

(1), тогда  явл-ся точностью оценки. Эту точность невозможно опре-ть по соотнош-ю (1). Поступают след. образом:=0.95;0.975;0.99

Она называется доверительной вероятностью или надежностью и потребуют вып-я (2)

(2)     Р()=.

Т.к. выборка является случайной, то инт.оценка также явл-ся случайной, поэтому можно говорить о вероятности этой инт. оценки. границы дов. интервала также явл-ся СВ.

Общая схема постр-я довер. инт-ла:

1.Из генер. сов-ти с известн. законом распр-я F(x, )  или f(x, )  СВ Х извл-ся выборка объема U, где

неизв. параметр.

2. По выборке опред.точечн. оценку этого параметра.

3. строится ф-я К зависит от  и оценки , назыв-ся статистикой и удовл-я след. св-вам: (К())

4.Задается доверит. вероят-ть  или Ур-нь знач-ти

5.Исп-я закон распред-я стат.  находят 2 значения К1 и К2, удовл. след. условию: Р(К1<К()<К2)=

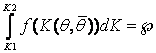
К1 и К2 находим из след. условий:

Р(К<К()<К1)=;

Р(К<К()>К2)=;

(К1,К2) наз-ся доверит.интервалом.