40. Парная минимальная регрессия

Рассмотрим уравнение (1). для конкретных значений переем. у соотношение (1) записывается в виде(2) . тогда аналогом уравнения (2) яв-ся соотношение (3) , где ; ; ;

 и  наз-ся теоретическим коэффициентом ( параметром регреесии)

 и  коэффициенты регрессии;  - остатком

1);

2);

3)

метод основан на минимизации суммы квадратов отклонений называется методом наименьших квадратов

4) для нахождения неизвестного коэф регрессии можно использовать метод макс правдоподобия

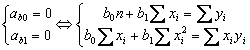
получим нормальную систему уравнений ; ;

;

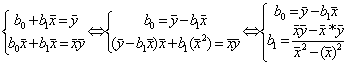
коэф  имеет размерность отношения размерностей переменной у как переем х. Он указывает измен перем у при возрастании знач х на одну единицу. В этом и состоит эконом смысл  

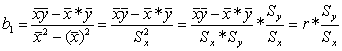
замечания: 1) метод наим квадр составлен так, что прямая регрессия  проходит через точку х ср и у ср; 2)  и  назыв оценками наим квдр; 3) мнк оценки яв-ся точечными оценками неизвестн парам регрессии  и ; 4) мнк оценки яв-ся фу-ями выборки, что позволяет их легко рассчитать; 5) случ отклонения  некоррелированы со значениями переем х (); 6) случ отклонение  некоррелированы со значен перем у() ; 7) условие назыв условием идентифицируемости регрессионной модели (3). Это означает что не все наблюдения перемен х совпадают между собой; 8) назыв остаточной суммой квадр.