8. Функция распределения вероятностей СВ.
Функцией
распределения(интегральным законом) вер. СВ называется вероятность того, что СВ
Х примет значение меньшее, чем действ. число Х(Х![]()
![]() )
)
F(X)=P(X<x)
Функц. распределения опис. СВ свероятн. точки зрения, поэтому ее можно рассм-ть, как 1 из видов закона распред-я СВ.
Если СВ Х рассм-ть как случ.
точку на плоскости, то функция распред-я означ. вероятность того, что случ.
точка лежит левее начисловой прямой, чем заранее задан. т. Х. Если Х дискретная
СВ, то F(X)=
![]()
1. 0![]()
2. P(![]() )
= F(
)
= F(![]() )
– F(
)
– F(![]() )
)
Следствие. Если Х- НСВ, то
P(![]() )
= P(
)
= P(![]() )
= P(
)
= P(![]() )
= P(
)
= P(![]() )
= F(
)
= F(![]() )
– F(
)
– F(![]() ).
).
3. Если Х2>Х1, то
F(X2)![]() F(X1)
F(X1)
4.Функция распр-я непрерывна слева.
5.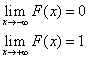
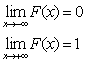
СВ Х называется непрерывной, если ее функция распред-я непрерывна при всех значениях Х.
СВ Х называется непрерывной, если ее кажд. значение им. нулевую вероятность.
Замечание: функция распред-я СВ Х ставит кажд. возможному значению (Хр) вероятность р:
F(Xp)=p
Значение Хр для кот. вып-ся указ. равенство называется квантилью.