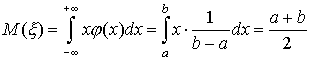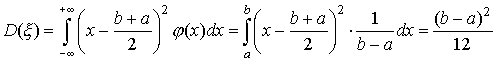Классическое определение вероятности.

Пример 1. На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не удовлетворяющих стандарту. Определить вероятность P(A) того, что взятый наудачу подшипник окажется стандартным.

   Решение: Число стандартных подшипников равно 1000—30=970. Будем считать, что каждый подшипник имеет одинаковую вероятность быть выбранным. Тогда полная группа событий состоит из N=1000 равновероятных исходов, из которых событию A благоприятствуют М=970 исходов. Поэтому P(A)=M/N=970/1000=0.97

   Пример 2. В урне 10 шаров: 3 белых и 7 черных. Из урны вынимают сразу два шара. Какова вероятность р того, что оба шара окажутся белыми?

   Решение: Число N всех равновероятных исходов испытания равно числу способов, которыми можно из 10 шаров вынуть два, т. е. числу сочетаний из 10 элементов по 2:

   Число благоприятствующи исходов:

   Следовательно, искомая вероятность

Пример 3. В урне 2 зеленых, 7 красных, 5 коричневых и 10 белых шаров. Какова вероятность появления цветного шара?

   Решение: Находим соответственно вероятности появления зеленого, красного и коричневого шаров:
Р(зел.)=2/24; Р(кр.)=7/24; Р(кор.)=5/24. Так как рассматриваемые события, очевидно, несовместны, то, применяя аксиому сложения, найдем вероятность появления цветного шара:

Условная вероятность. Теорема умножения вероятностей.

   Пример 1. Какова вероятность того, что при десятикратном бросании монеты герб выпадет 10 раз ?

   Решение: Пусть событие Ai — появление герба при i-м бросании. Искомая вероятность есть вероятность совмещения всех событий Ai (i=1,2,3,...,10), а так как они, очевидно, независимы в совокупности, то применяя формулу (10), имеем
 

   Но P(Ai)=1/2 для любого i; поэтому

Пример 2. Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что в течение часа станок не потребует внимания рабочего, для первого станка равна 0,9, для второго — 0,8, для третьего — 0,7. Найти: 1) вероятность р того, что в течение часа ни один из трех станков не потребует внимания рабочего; 2) вероятность того, что в течение часа по крайней мере один из станков не потребует внимания рабочего.

   Решение:
   1) Искомую вероятность р находим по формуле (10):
 

   2) Вероятность того, что в течение часа станок потребует внимания рабочего для первого станка равна 1—0,9=0,1, для второго и для третьего станков она соответственно равна 1—0,8=0,2 и 1—0,7=0,3. Тогда вероятность того, что в течение часа все три станка потребуют внимания рабочего, на основании формулы (10) составляет
 

   Событие A, заключающееся в том, что в течение часа все три станка потребуют внимания рабочего, противоположно событию , состоящему в том, что по крайней мере один из станков не потребует внимания рабочего. Поэтому по формуле (3) получаем
 

Пример 3. Из урны, содержащей 3 белых и 7 черных шаров, вынимают два шара. Какова вероятность того, что оба шара окажутся белыми ?

   Решение: Эта задача уже была решена в п. 3 с помощью классического определения вероятности. Решим ее, применяя формулу (5). Извлечение двух шаров равносильно последовательному их извлечению. Обозначим через А появление белого шара при первом извлечении, а через В — при втором. Событие, состоящее в появлении двух белых шаров, является совмещением событий А и В. По формуле (5) имеем
 

   Но Р(А)=3/10; РA(В)=2/9, поскольку после того, как был вынут первый белый шар, в урне осталось 9 шаров, из которых 2 белых. Следовательно,
 

Формула полной вероятности.

   Пример. В магазин поступили электрические лампочки одного типа, изготовленные на четырех ламповых заводах: с 1-го завода 250 шт., со 2-го — 525 шт., с 3-го — 275 шт. и с 4-го — 950 шт. Вероятность того, что лампочка прогорит более 1500 часов, для 1-го завода равна 0,15, для 2-го — 0,30, для 3-го — 0,20, для 4-го — 0,10. При раскладке по полкам магазина лампочки были перемешаны. Какова вероятность того, что купленная лампочка прогорит более 1500 часов?

   Решение: Пусть A — событие, состоящее в том, что лампочка прогорит более 1500 часов, а Н1, Н2, Н3 и Н4 — гипотезы, что она изготовлена соответственно 1, 2, 3 или 4-м заводом. Так как всего лампочек 2000 шт., то вероятности гипотез соответственно равны

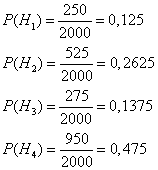
   Далее, из условия задачи следует, что

   Используя формулу полной вероятности (11), имеем

Формула Бейеса.

   Пример. На склад поступило 1000 подшипников. Из них 200 изготовлены на 1-м заводе, 460—на 2-м и 340 - на 3-м. Вероятность того, что подшипник окажется нестандартным, для 1-го завода равна 0,03, для 2-го — 0,02, для 3-го — 0,01. Взятый наудачу подшипник оказался н естандартным. Какова вероятность того, что он изготовлен 1-м заводом?

   Решение: Пусть A — событие, состоящее в том, что взятый Подшипник нестандартный, а - гипотезы, что он изготовлен соответственно 1-м, 2-м или 3-м заводом. Вероятности указанных гипотез составляют

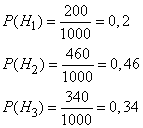
   Из условия задачи следует, что

   Найдем , т. е. вероятность того, что подшипник, оказавшийся нестандартным, изготовлен 1-м заводом. По формуле Бейеса имеем

   Таким образом, вероятность гипотезы, что подшипник изготовлен 1-м заводом, изменилась после того, как стало известно, что он нестандартен.

ПОСЛЕДОВАТЕЛЬНЫЕ ИСПЫТАНИЯ. ФОРМУЛА БЕРНУЛЛИ.

   Пример 2. Определить наивероятнейшее число попаданий в цель в примере 1.

   Решение: Здесь
   n=8;
   p=0,6;
   q=0,4;
   np-q=8*0,6-0,4=4,4;
   np+p=8*0,6+0,6=5,4.

   Согласно формуле (14) наивероятнейшее значение лежит на сегменте [4.4;5.4] и, следовательно равно 5.

  Пример 3. Игральную кость бросают 80 раз. Определить вероятность того, что цифра 3 появится 20 раз.

   Решение: Здесь
   m=20;
   n=80;
   p=1/6;
   q=1-1/6=5/6;

   далее находим

   Используя формулу (15), получим

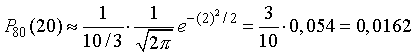
   так как из Таблица I. Находим  что

Дискретные случайные величины.

   Пример 1. Случайная величина — число очков, выпадающих при однократном бросании игральной кости. Возможные значения — числа 1, 2, 3, 4, 5 и 6. При этом вероятность того, что примет любое из этих значений, одна и та же и равна 1/6. Какой будет закон распределения ?

   Решение: Таким образом, здесь закон распределения вероятностей есть функция р(х)=1/6 для любого значения х из множества {1, 2, 3, 4, 5, 6}.

Пример 3. На завод прибыла партия деталей в количестве 1000 шт. Вероятность того, что деталь окажется бракованной, равна 0,001. Какова вероятность того, что среди прибывших деталей будет 5 бракованных?

   Решение:

   Здесь .

   По формуле (17) находим

Функция распределения вероятностей случайной величины и ее свойства.

   Пример 1. Найти функцию распределения случайной величины , приведенной в примере 1, п. 1.

   Решение: Ясно, что если , то F(x)=0, так как не принимает значений, меньших единицы. Если , то ; если , то . Но событие <3 в данном случае является суммой двух несовместных событий: =1 и =2. Следовательно,

   Итак для имеем F(x)=1/3. Аналогично вычисляются значения функции в промежудках , и . Наконец, если x>6 то F(x)=1, так как в этом случае любое возможное значение (1, 2, 3, 4, 5, 6) меньше, чем x. График функции F(x) изображен на рис. 4.
 

   Пример 2. Найти функцию распределения случайной величины , приведенной в примере 2, п. 1.

   Решение: Очевидно, что

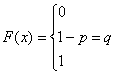
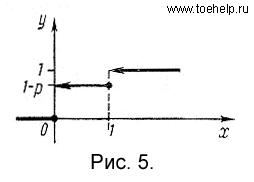
   График F(x) изображен на рис. 5.
 

Нормальное распределение.

   Пример 1. Пусть случайная величина подчиняется нормальному закону распределения вероятностей с параметрами a=0, =2.
   Определить:
      1) ;
      2) ;

   Решение:
      1) Используя формулу (32), имеем

   Из табл. II находим, что Ф(1)=0,34134, Ф(1,5)=0,43319. Следовательно
 

      2) Так как a=0, то . По формуле (33) находим
 

Нормальное распределение.

   Пример 2. В каких пределах должна изменяться случайная величина, подчиняющаяся нормальному закону распределения, чтобы

   Решение: По формуле (33) имеем

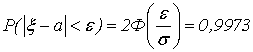
   Следовательно, . Из табл. II находим, что этому значению соответствует , откуда

Дисперсия и ее свойства. Среднее квадратическое отклонение.

   Пример 1. Cлучайная величина - число очков, выпадающих при однократном бросании игральной кости (см. § 3, п.1, пример 1). Определить: математическое ожидание, дисперсию и средне квадратическое отклонение

   Решение:

    Используя формулы (39), (44) и (49) соответственно получим

Пример 2. Cлучайная величина - число наступления события A при одном испытании, причем P(A)=p (см. § 3, п.1, пример 2). Найти математическое ожидание и дисперсию.

   Решение:

   Величина принимает два значения 0 и 1 соответственно с вероятностями q=1-p и p. Поэтому по формулам (39) и (44) находим
 

Пример 3. Cлучайная величина m - число наступления события A в n независимых опытах, причем вероятность наступления события A в каждом опыте равна p. Найти M(m), D(m) и

   Решение:

   Пусть - случайная величина, принимающая значения 1 или 0 в зависимости от того, происходит или не происходит событие A в i-м опыте. Тогда . Ясно, что попарно независимы. Из результата примера 2 следует, что , для любого i. На основании свойства 3° для математического ожидания и дисперсии имеем
 

   Пример 4. Пусть - случайная величина распределенная по закону Пуассона

[См. формулу (17)]. Найти:

   Решение:

   Используя соотношение (39), получим
 

   Так как
 

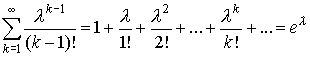
Пример 5. Пусть - случайная величина, имеющая равномерное распределение с плотностью

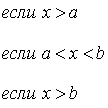
[См. формулу (27)]. Найти математическое ожидание, дисперсию и средне квадратическое отклонение cлучайной величины.

   Решение:

    По формулам (40), (45) и (49) находим